Paper Summary #7 - Efficient Transformers: A Survey

Paper: Efficient Transformers: A Survey
Link: https://arxiv.org/abs/2009.06732
Authors: Yi Tay, Mostafa Dehghani, Dara Bahri, Donald Metzler
I wanted to summarize this paper for a long time now because of the immense amount of information in this paper. Thanks to the Cohere For AI community for having a session on this paper which made me revisit this.
What?
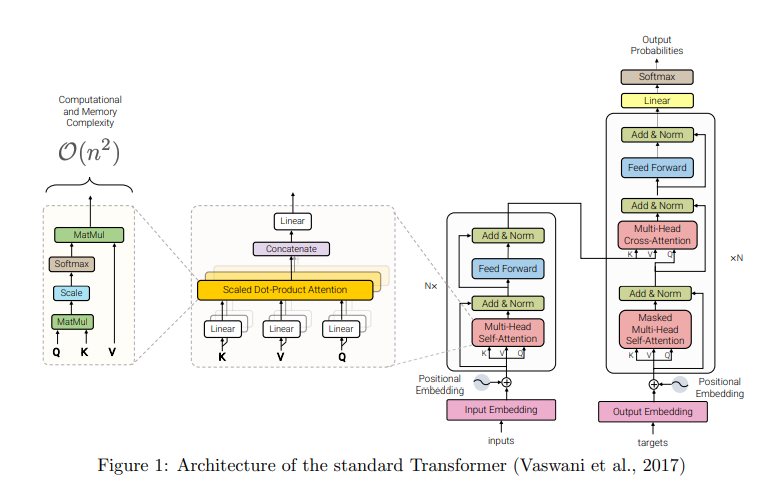
This is a survey paper on the various memory-efficiency based improvements on the original Transformers architecture by Vaswani et al. But wait, for those unaware, how is the Transformers architecture inefficient?
- The attention operation has a quadratic complexity over the sequence length L, also sometimes represented using N (since each token attends to other set of tokens in the sequence)
- The Attention operation of \(QK^T\) uses \(N^2\) time and memory. Here (in no-batching case) $Q, K, V$ (query, key and value matrices) have dimensions \(N \times d\) where \(d\) is the dimension of query, key and value vectors.
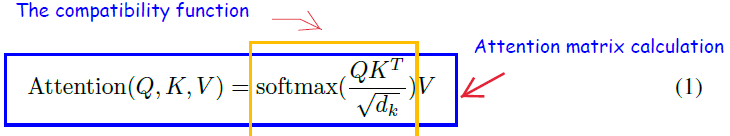
Memory-Efficient Transformers
Low-Rank methods
Linformer - https://arxiv.org/abs/2006.04768
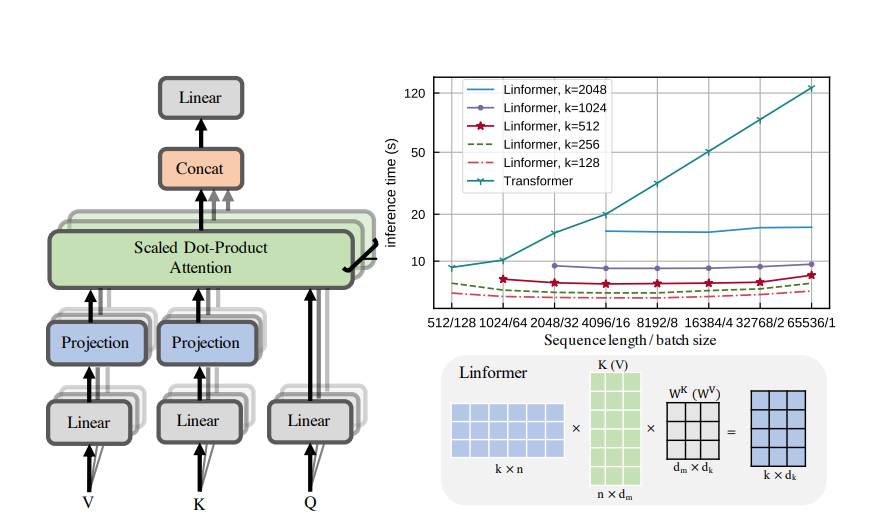
In Linformer, the original Key and Value matrices are projected from \(N \times d\) to a reduced \(k \times d\).

The above operations only require \(O(N * k)\) time and space complexity. Thus, if we can choose a very small projected dimension \(k\), such that \(k \lt\lt N\), then we can significantly reduce the memory and space consumption.
Performer - https://arxiv.org/abs/2009.14794
The goal in the Performer paper was to reduce the complexity of attention calculation \((QK^T)V\) of \(O(L^2 * d)\) to \(O(L * d^2)\) by transforming the order of operations and using a kernel operation to approximate the softmax operation so that the order of operations can be changed.
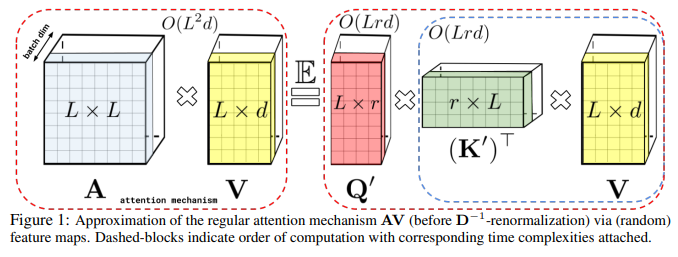
From, a great blog on the Performer paper -
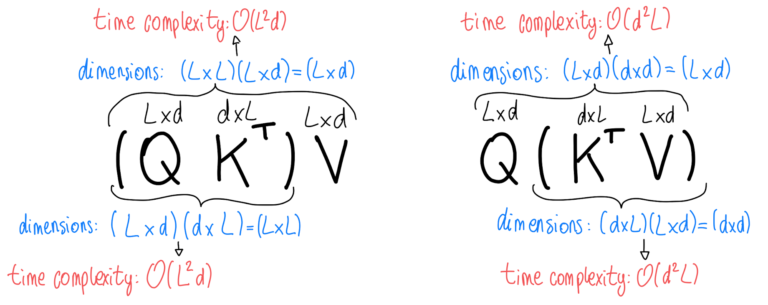

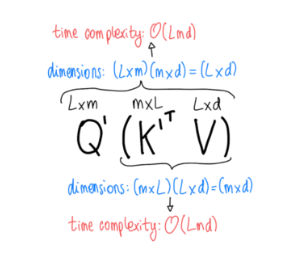
Learnable Patterns
Clustered Attention - https://arxiv.org/abs/2007.04825 + https://clustered-transformers.github.io/blog/
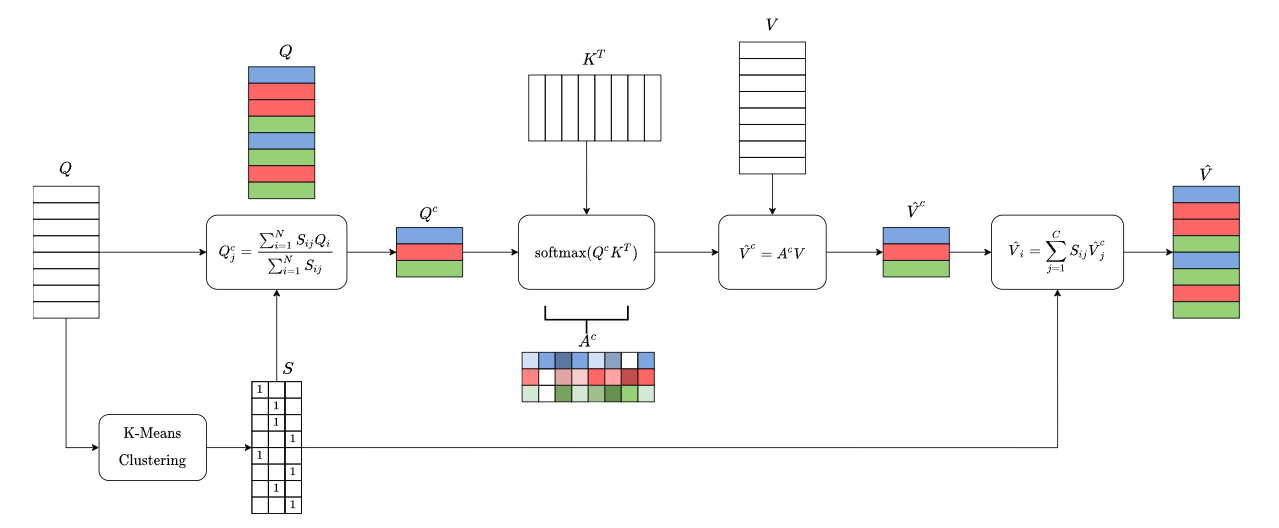
- First cluster the queries into non-overlapping clusters.
- Attention weights \(A^c\) are computed using the centroids instead of computing them for every query
- Use clustered attention weights \(A^c\) to compute new Values \(V^c\)
- Use the same attention weights and new values for queries that belong to same cluster.
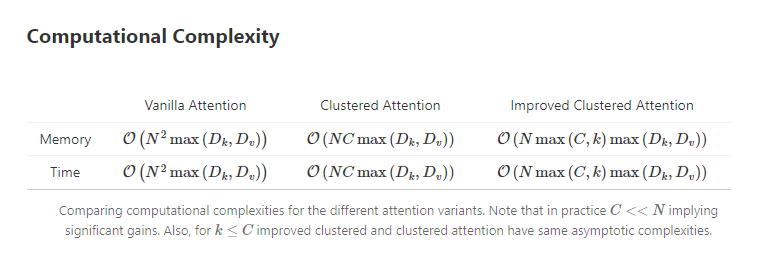
- Computational complexity becomes \(O(N * C * max(D_k, D_v))\)
They also propose an Improved Clustered Attention in their blog. The complexity comaprisons are here -
Reformer - https://arxiv.org/abs/2001.04451
Uses the concept of Locality sensitive hashing (LSH) attention, where the goal is to not store the entire \(QK^T\) matrix but only the \(\textrm{softmax}(QK^T)\), which is dominated by the largest elements in a typically sparse matrix. For each query \(q\) we only need to pay attention to the keys \(k\) that are closest to \(q\). For example, if \(k\) is of length 64K, for each \(q\) we could only consider a small subset of the 32 or 64 closest keys. So the attention mechanism finds the nearest neighbor keys of a query but in an inefficient manner.
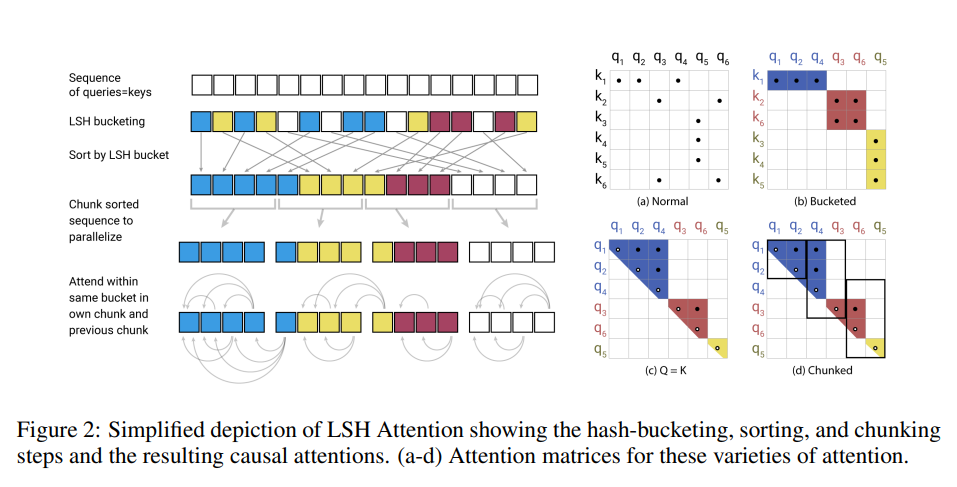
- Calcluate LSH hashes of Queries and Keys (\(Q\) and \(K\))
- Make chunks and compute attention only for vectors in the same bucket
The paper also introduces the concept of Reversible residual networks (RevNets). In the residual connections in Transformers, one needs to store the activations in each layer in memory in order to calculate gradients during backpropagation. RevNets are composed of a series of reversible blocks. In RevNet, each layer’s activations can be reconstructed exactly from the subsequent layer’s activations, which enables us to perform backpropagation without storing the activations in memory.
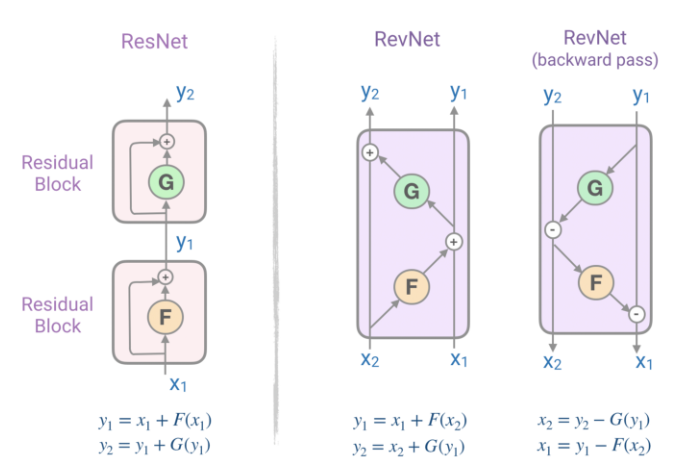
Reformer applies the RevNet idea to the Transformer by combining the attention and feed-forward layers inside the RevNet block. Now F becomes an attention layer and G becomes the feed-forward layer:

The reversible residual layers allows storing activations only once during the training process instead of N times.
The memory complexity of Reformer is \(O(N * log(N))\).
Memory-based
Big Bird https://arxiv.org/abs/2007.14062 + https://huggingface.co/blog/big-bird
BigBird relies on block sparse attention and can handle sequences up to a length of 4096 at a much lower computational cost compared to BERT. It has achieved SOTA on various tasks involving very long sequences such as long documents summarization, question-answering with long contexts.
BigBird proposes three ways of allowing long-term attention dependencies while staying computationally efficient -
- Global attention - Introduce some tokens which will attend to every token and which are attended by every token. The authors call this the ‘internal transformer construction (ITC)’ in which a subset of indices is selected as global tokens. This can be interpreted as a model-memory-based approach.
- Sliding attention - Tokens close to each other, attend together. In BigBird, each query attends to \(w/2\) tokens to the left and \(w/2\) tokens to the right. This corresponds to a fixed pattern (FP) approach.
- Random attention - Select some tokens randomly which will transfer information by transferring to other tokens which in turn can transfer to other tokens. This may reduce the cost of information travel from one token to other. Each query attends to r random keys. This pattern is fixed
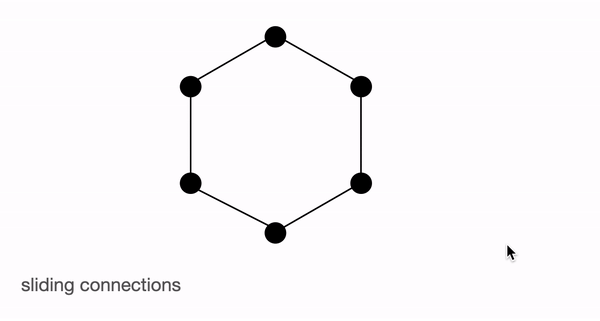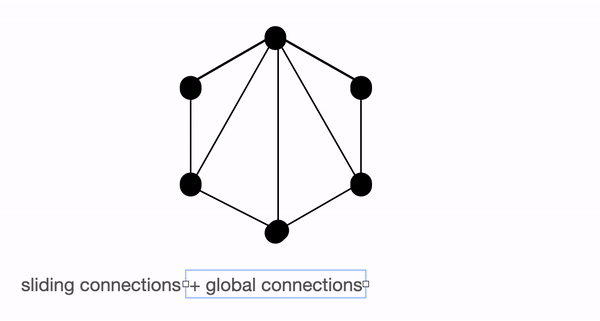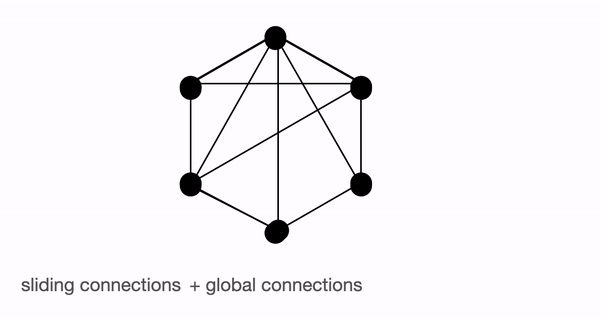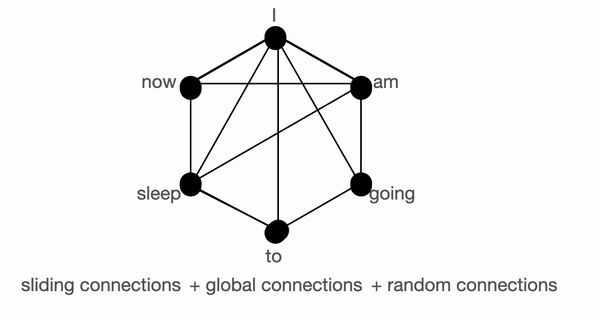
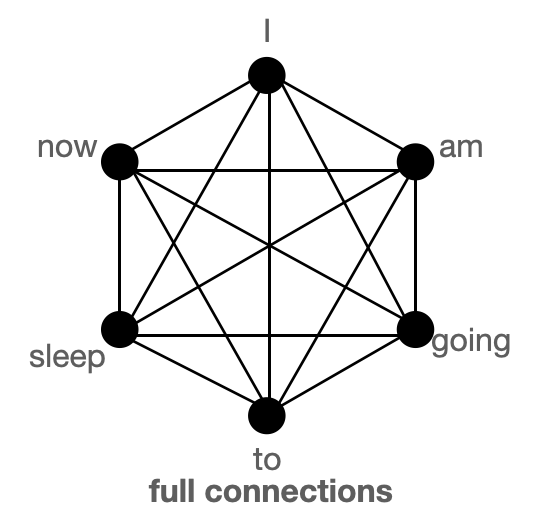
BigBird block sparse attention is a combination of sliding, global & random connections (total 10 connections) as shown in gif above. While a graph of normal attention (bottom) will have all 15 connections (note: total 6 nodes are present). One can simply think of normal attention as all the tokens attending globally.
The attention calculation in BigBird is slightly complex and I would refer to the Huggingface blog for it -
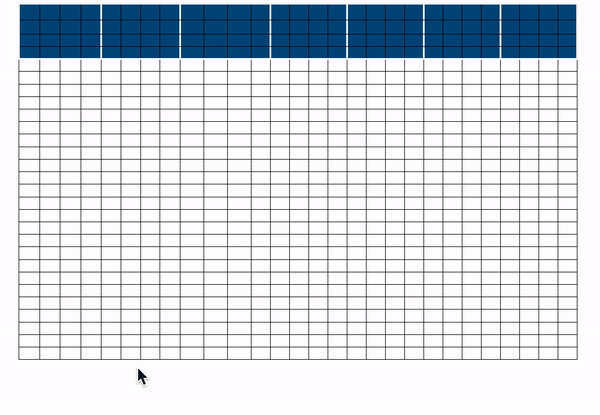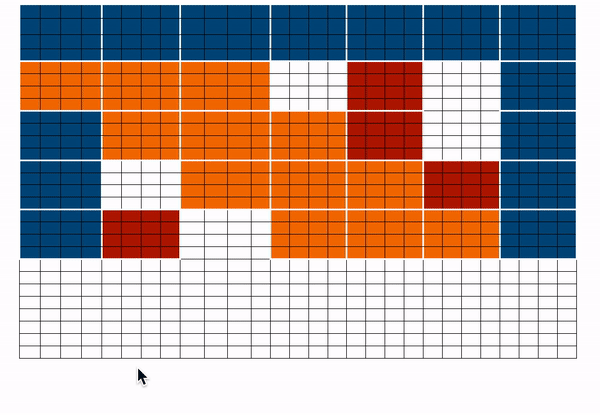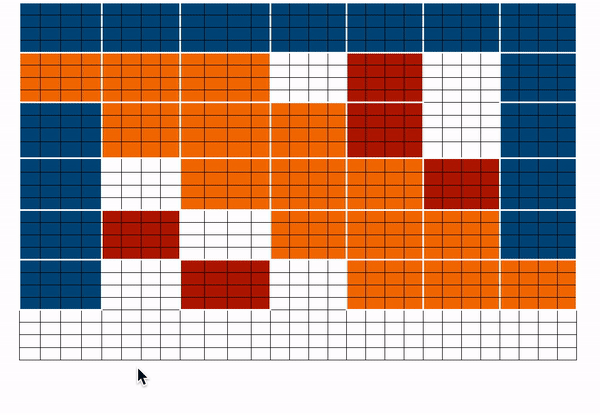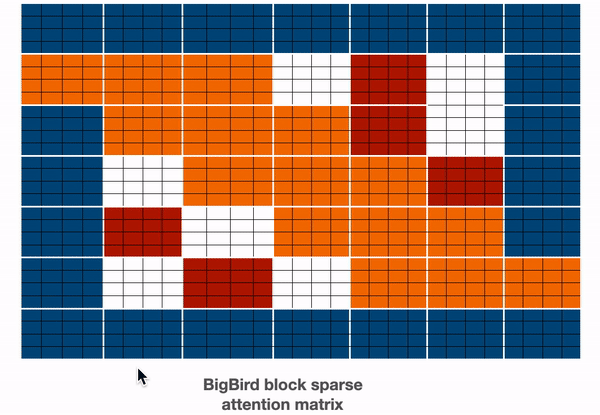
The memory complexity of the self-attention is linear, i.e., \(O(N)\). The BigBird model does not introduce new parameters beyond the Transformer model.
Complexity Summary of various models
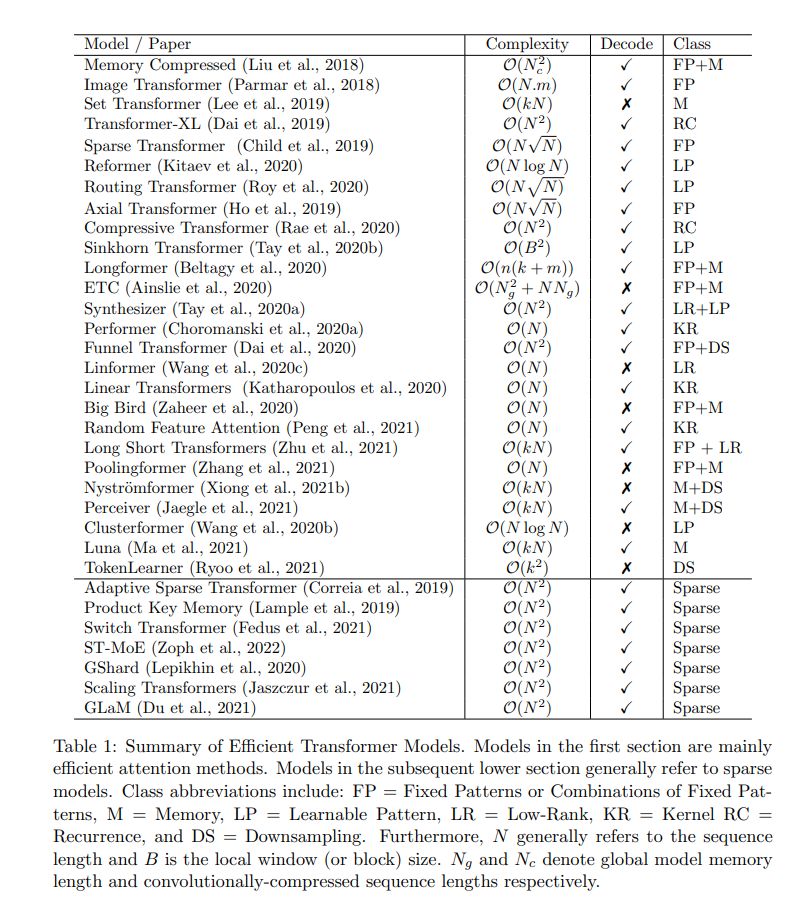
There are many more papers discussed in the survey. I will add their summaries here as I go through them.