Notes from GTC'25: CUDA Techniques to Maximize Compute and Instruction Throughput

You can watch the talk here - link
GPU Basics
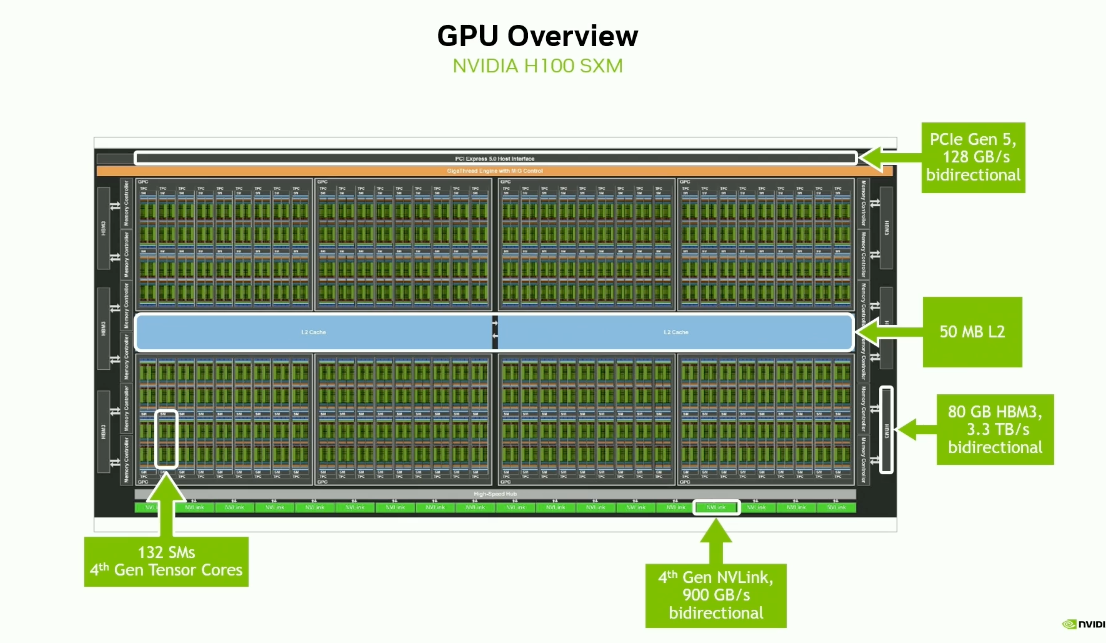
PCIe is used for communication between the CPU and the GPU.
NVLink is used for communication between the GPUs.
Each SM of Hopper architecture has -
- 4 sub-partitions
- 128 FP32 units
- 64 FP64 units
- 64 INT32 units
- 4 mixed-precision Tensor Cores
- 16 special function units
- 4 warp schedulers
- 32 load/store units
- 64K 32-bit registers
- 256KB unified L1 cache and shared memory (however on checking CUDA device properties, I found that the shared memory is 228 KB)
- Tensor Memory Accelerator (TMA)

In Hopper, in addition to blocks and grids, there is an optional level in the thread hierarchy called - Thread Block Clusters. Thread blocks in a cluster are guaranteed to be concurrently scheduled and enable efficient cooperation and data sharing for threads across multiple SMs.
GPUs follow SIMT (Single Instruction, Multiple Threads) execution.
- Each thread has its own program counter.
- SIMT = SIMD + Program Counters
Since Volta, each thread has its own program counter.
Warp Divergence
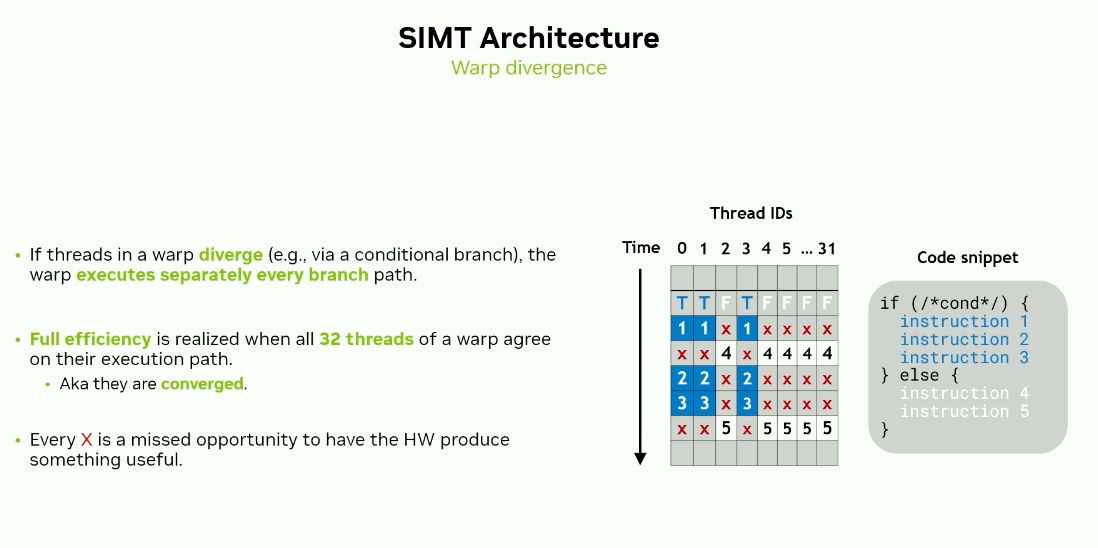
Metrics to look at (in NCU) to detect divergence:
- Average Predicated-On Threads Executed
- At this instruction, how converged is my warp on average?
- Divergent Branches
- Number of times branch target differed
- (Soon) Derivative Average Predicated-On Threads Executed
- E.g. if in a piece of code - At to level, it diverges slightly (but only once) and stays diverged; and in lower level code, there is frequent divergence and re-convergence although less severely. Then,
- Derivative metric has higher value for the top level divergence.
- Divergent Branch metric has higher value for the lower level code.
- E.g. if in a piece of code - At to level, it diverges slightly (but only once) and stays diverged; and in lower level code, there is frequent divergence and re-convergence although less severely. Then,
Tips for reducing warp divergence
Causes and solutions
- If per thread work is different - Queue and bin/sort the work
- If per thread work is discovered at different times - Queue the work
-
If per thread work ends at different times - Split into multiple kernels.
- Implement conceptual divergence via varying data, instead of varying control flow.
- Consider algorithmic / higher order changes to reduce divergence.
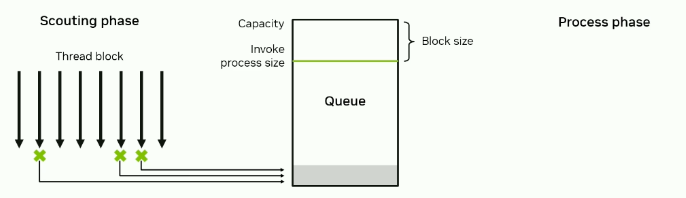
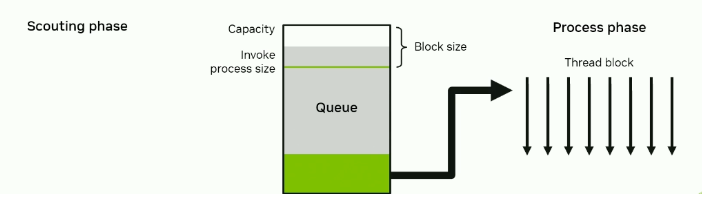
Work queueing in shared memory
There are workloads where an expensive computational calculation has a lightweight check to guard against it. A naive implementation may suffer from high divergence as not all threads will have work that passes the check.
Solution:
- When a threads finds a place to deep dive, add it to a queue and move on.
- Occasionally, all threads work simultaneously to clear the queue.
- Note: Threads that are finished scouting will then be used to help clear the queue.
Conceptual Divergence
Simple example:
float x = 0.0f;
if (isA) {
x = valA;
}
else if (isB) {
x = valB;
}
The above code has a divergence during assignment of value to x.
Conversion to conceptual divergence:
float x = (isA) * valA + (isB) * valB;
In this case, the result would be the same but we avoid the divergence by treating the boolean as scalar factors.
Warp scheduling and Kernel profiling
In Hopper,
- 4 warp schedulers per SM
- Each scheduler manages a pool of 16 warps
- In each clock cycle, each scheduler can issue an instruction for 1 warp.
Warp States
- Unused
- Active - Warp is resident on processor
- Stalled - Warp is waiting for previous instructions to complete; for input data of next instruction to be produced
- Eligible - All data, etc. the warp needs to execute the next instruction is available
- Selected - Eligible and selected by the scheduler to issue instruction in the cycle
Warp scheduler statistics
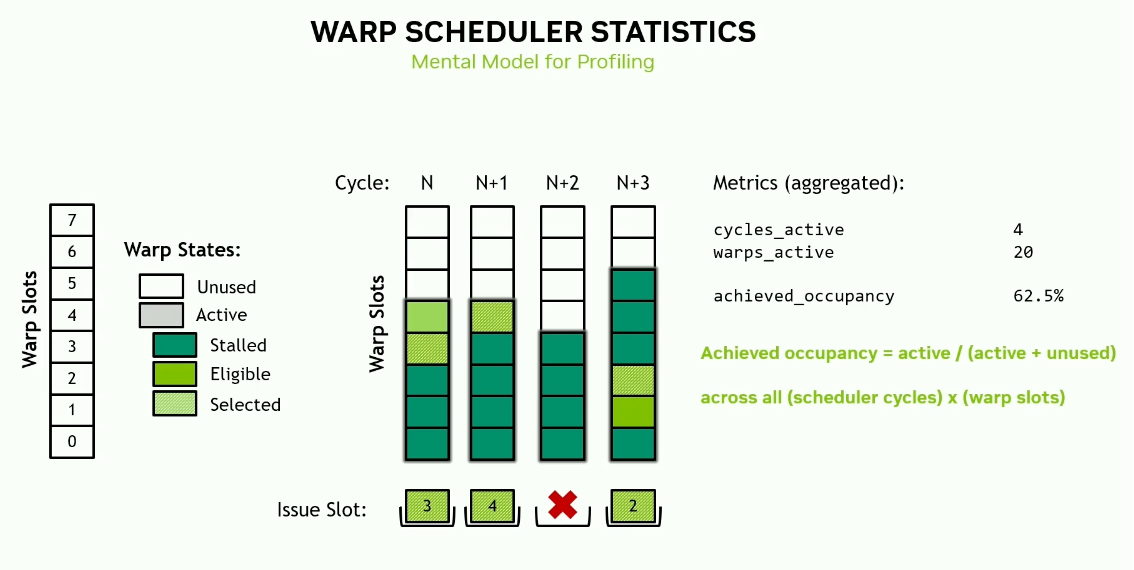
For a kernel launched with 32 threads and one block, performing addition of a scalar to each element of an array - assuming the addition takes 8 cycles, the warp statistics are -
- warps_active = 8/8 = 1 (per scheduler)
- warps_stalled = 7/8
- warps_eligible = 1/8
- warps_selected = 1/8
Context switching between warps is free from software perspective.
- Context is always resident on processor
- Switch is implemented in hardware
Kernel Profiling
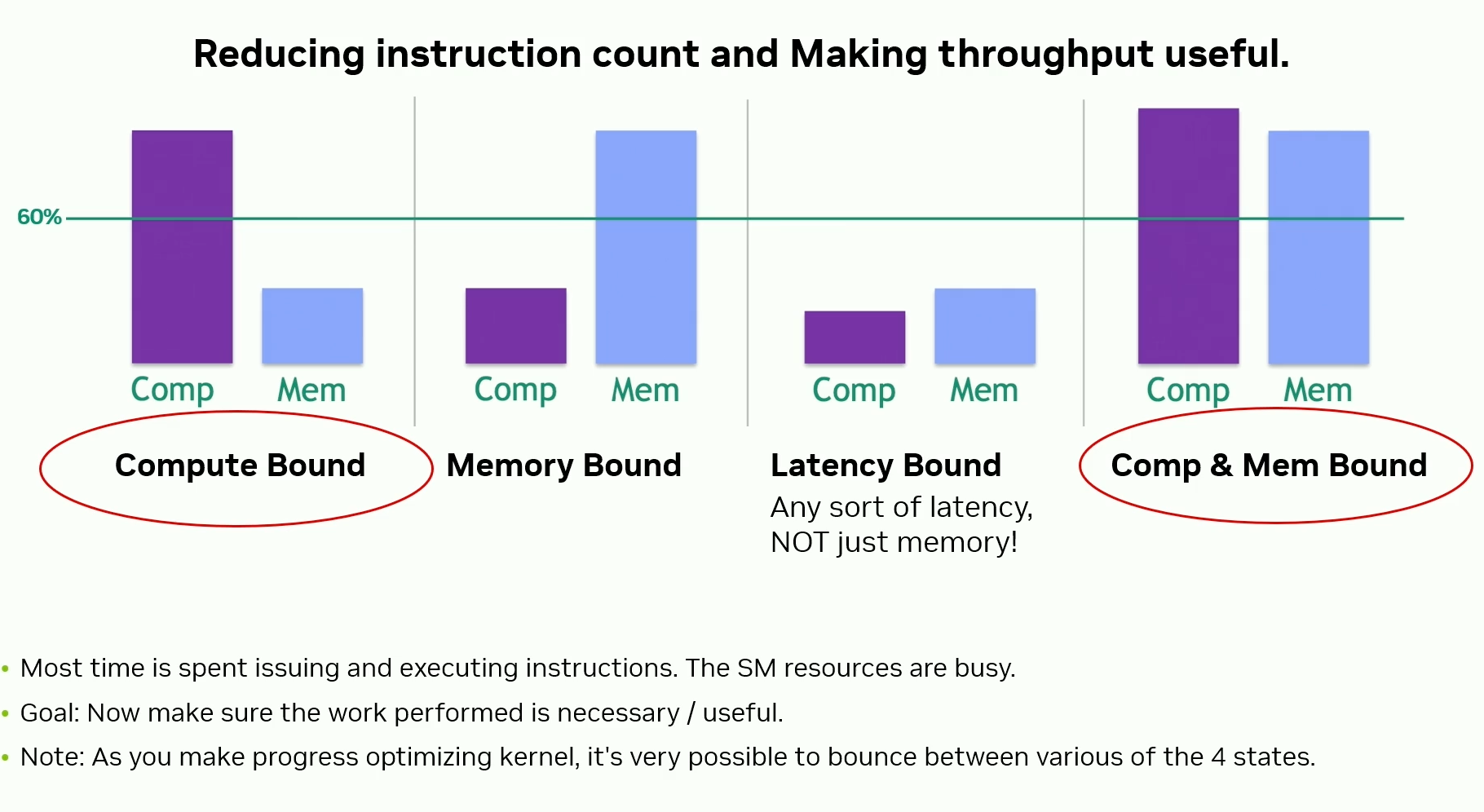
Compute Bound vs. Memory Bound vs. Latency Bound vs. Compute and Memory Bound
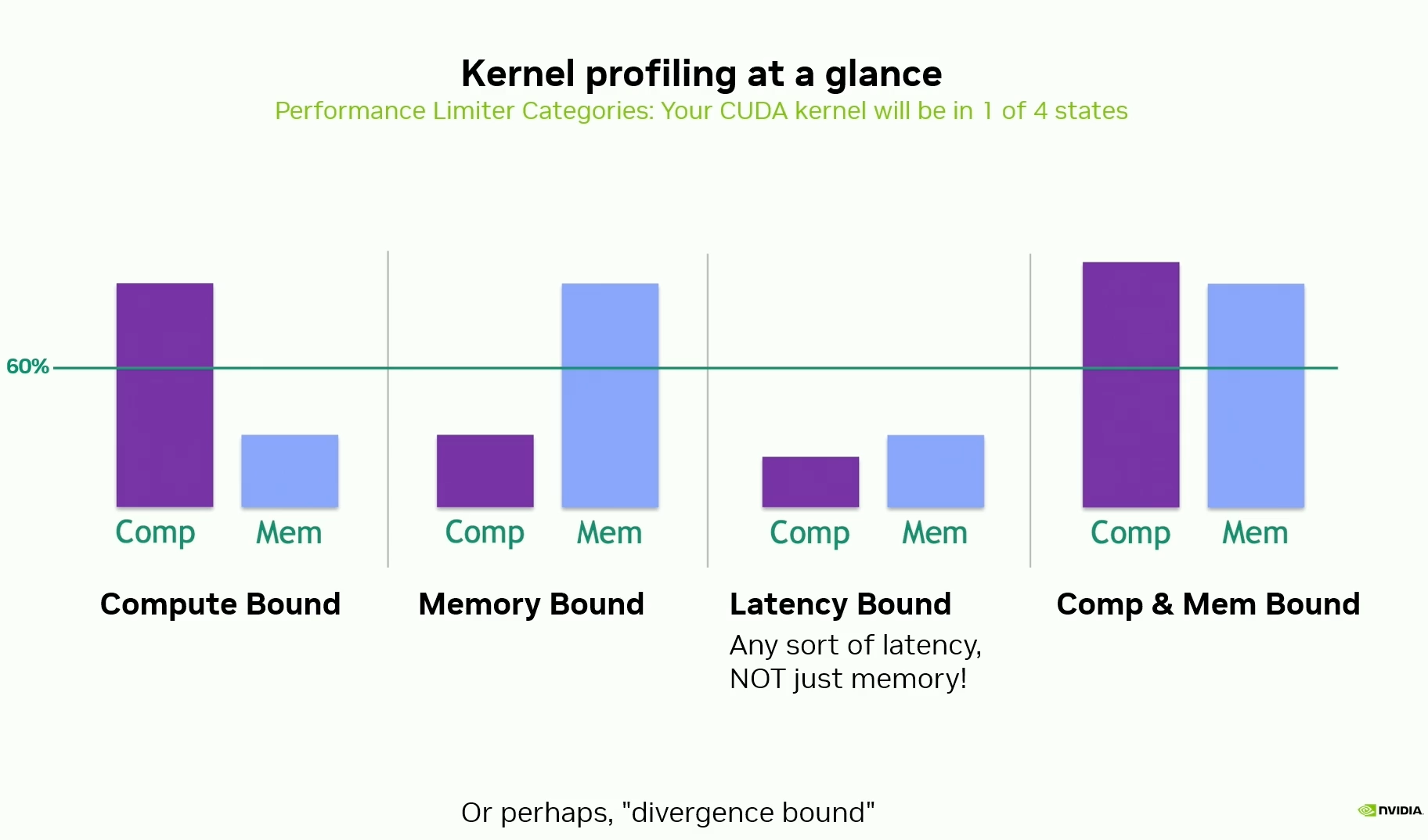
What to look for in NCU for each of these boundedness conditions -
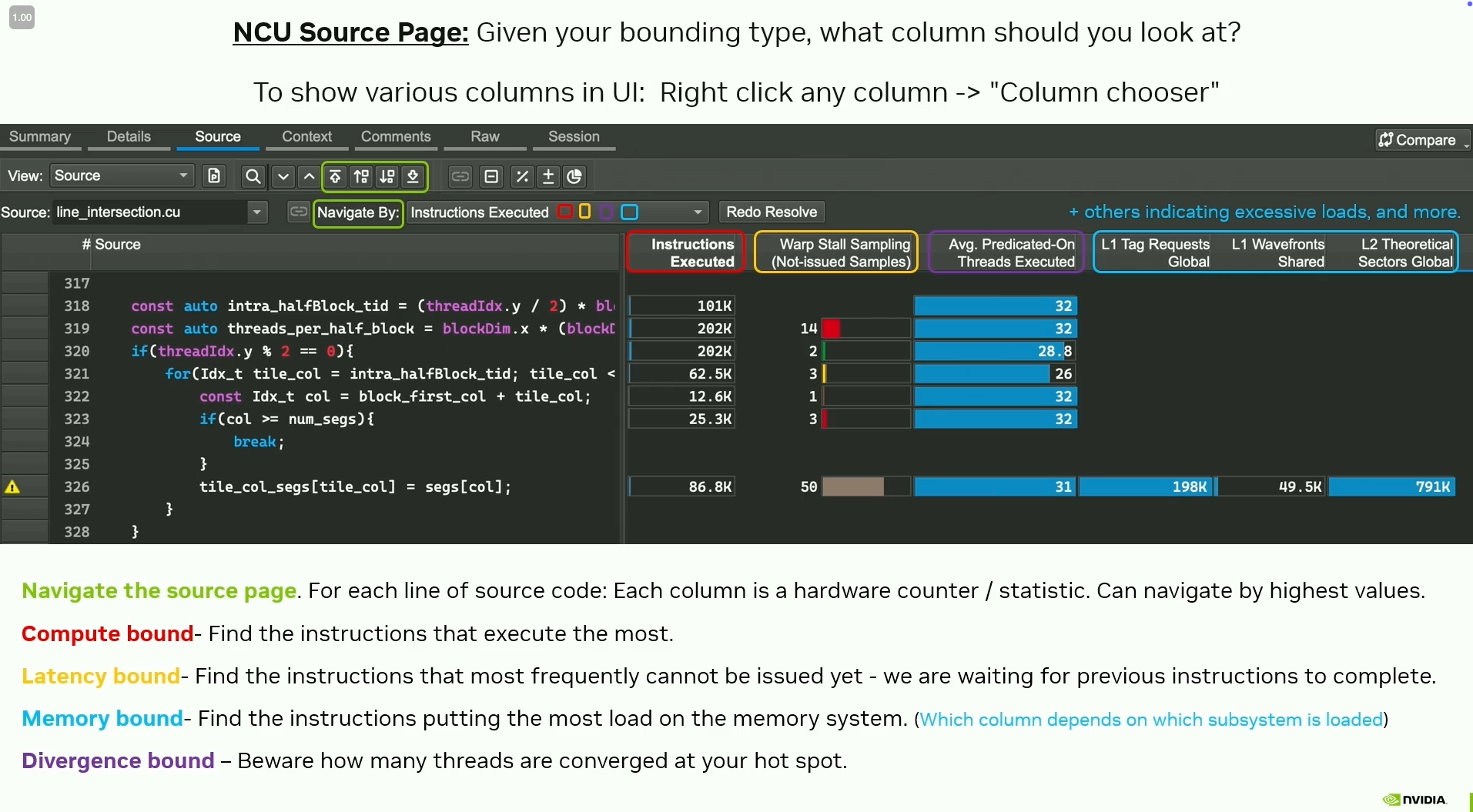
Latency hiding / Increasing instruction throughput
Most time is spent waiting for instructions to finish, and hardware resources are underutilized.
Need more instructions in flight at once to hide instruction latency and increase hardware utilization.
Types of stalls (warp stalls)
- Wait - Waiting for an instruction of compile-time-known latency
- Scoreboard - Waiting for an instruction of runtime-determined latency
- Long Scoreboard - typically associated with global memory
- Short Scoreboard - typically associated with shared memory
- Throttle - Waiting for the queue of a hardware resource to have free space
- Branch resolving - Waiting for branch / PC bookkeeping
- Barrier - Waiting for other threads to synchronize
Prefetching / Software / register pipelining is one way to hide latency.
Barriers
Barriers are a location in the code for threads to stop and wait for each other before moving on.
__syncthreads() syncs entire thread block. Required to be called by all the threads in the block. It cannot be called within conditionals unless they evaluate identically across thread block. Otherwise it has undefined behavior.
Cooperative Groups Sync - Syncs entire group defined by the user. Permitted to be called by only some threads and in divergent branches.
Increasing in-flight instructions
- Instruction Level Parallelism (ILP)
- Improve Occupancy - thread level parallelism
- Determines how many warps can run concurrently given HW resource constraints
- More concurrently active warps = more in-flight instructions
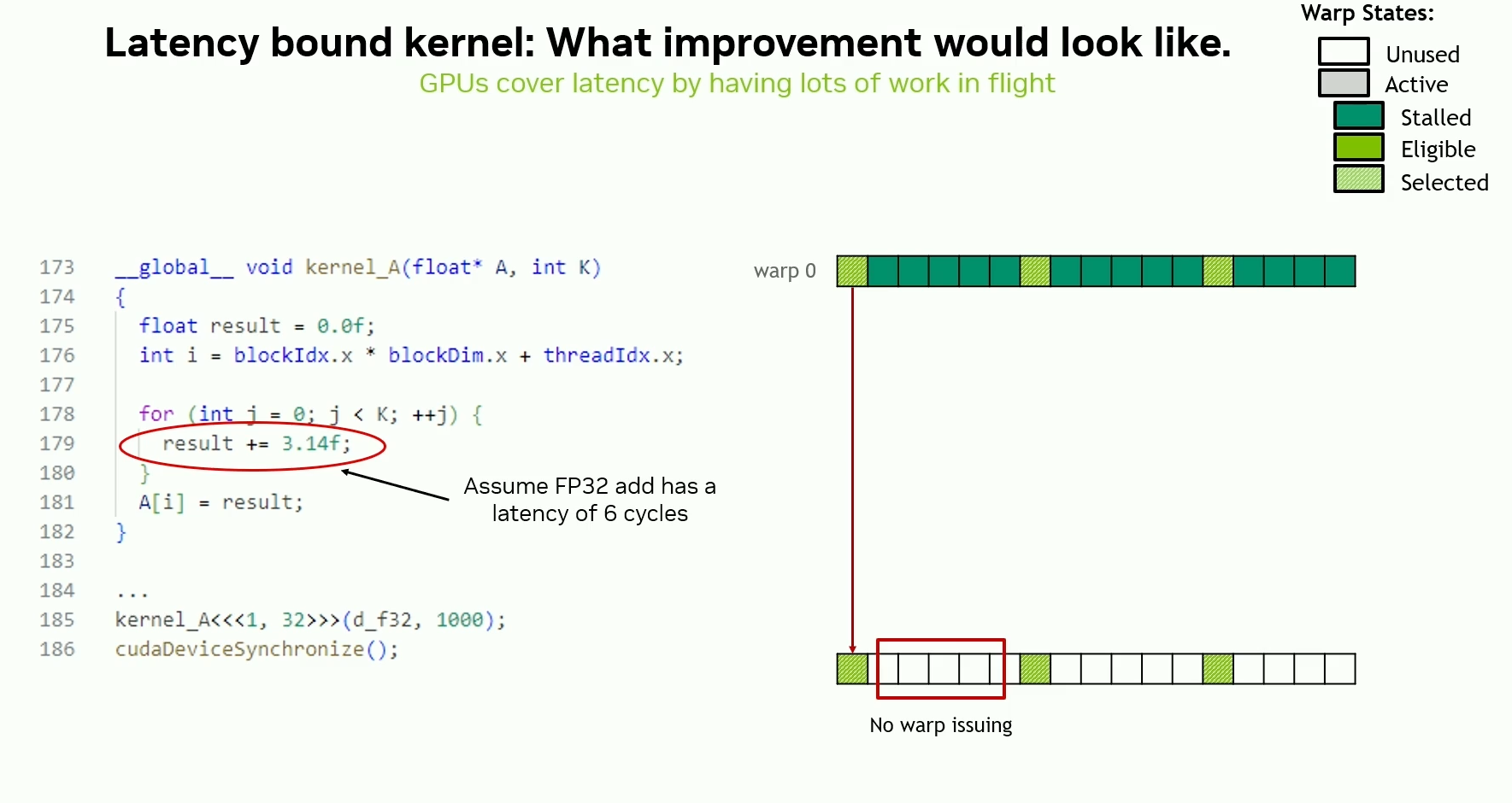

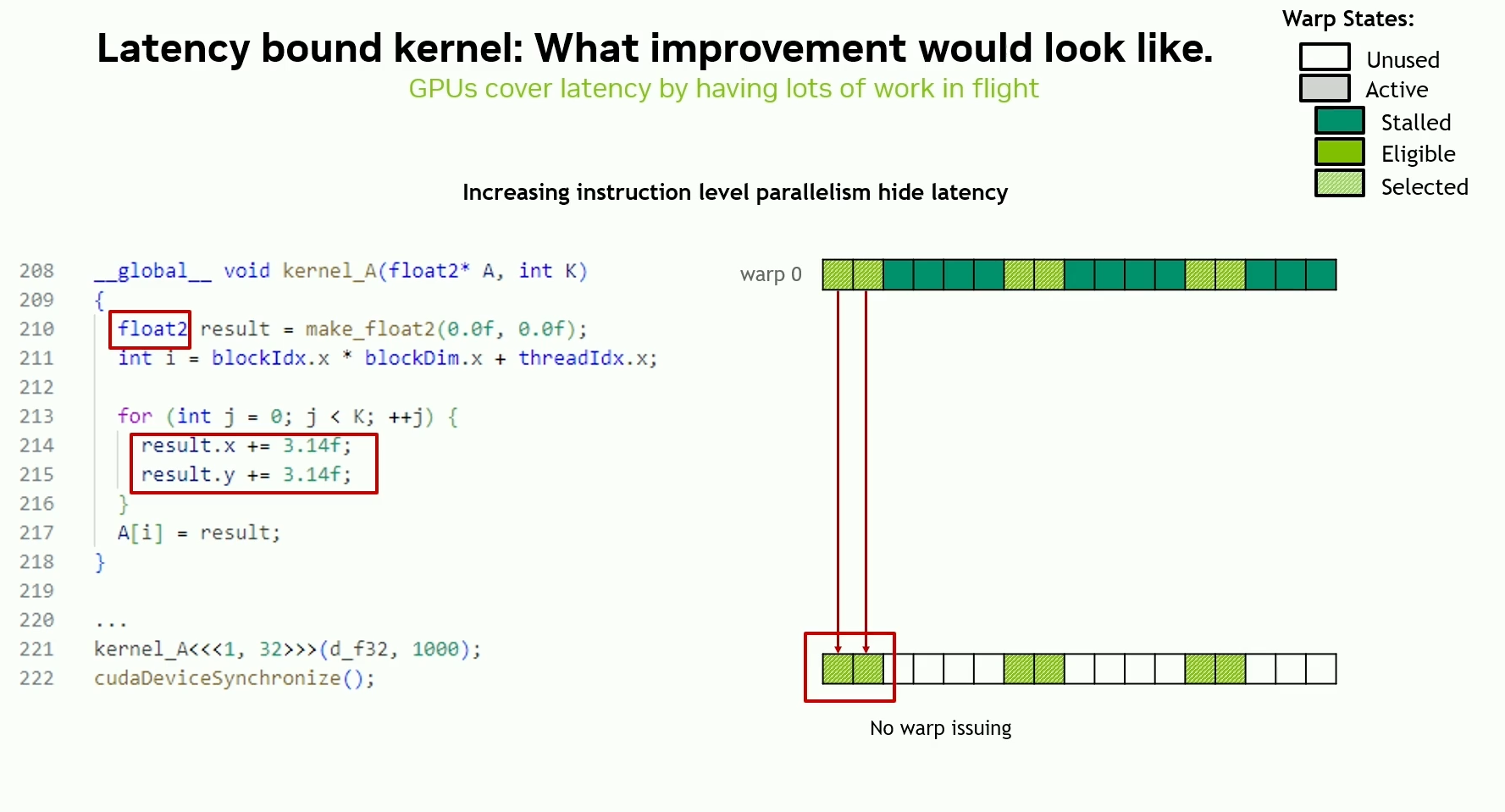
Essentially - more in-flight instructions, then more in-flight bytes.
Summary
If SM or Memory System resources are busy - don’t worry about stalls or unused issue slots. Issuing more frequently won’t help. Resources are already busy.
Otherwise, you are latency bound. Provide HW with more concurrent work. Try to -
- Issue more frequently
- Stall less frequently
- Busy yourself with something else during the stall
- Decrease duration of stall (use lower latency instructions)
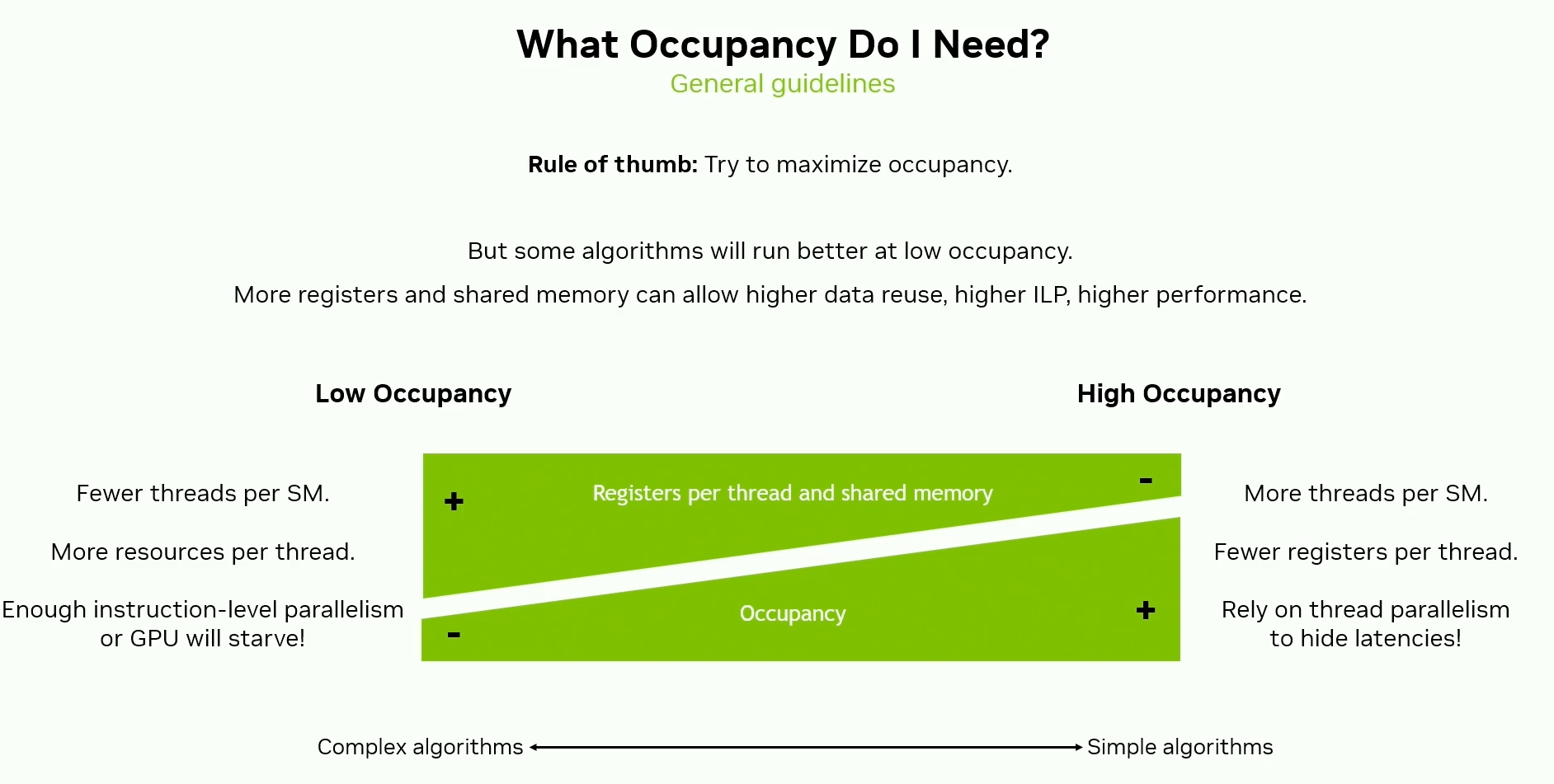
Occupancy
\[\text{Occupancy} = \frac{\text{Achievable # Active Warps per SM}}{\text{Device # Active Warps per SM}}\]Achievable occupancy of a CUDA kernel will be limited by at least one of several factors -
- SM resource assignment (shared memory, register partitioning; block size)
- Hardware factors - max blocks per SM, max warps per SM, etc.
Occupancy Limiters - Registers
To get report of register usage, compile with --ptxas-options=-v flag.
Maximum number of registers per thread can be set manually -
- At compile time using
--maxregcountflag of nvcc (per-file basis) - At runtime using
__launch_bounds__or__maxnreg__qualifiers (per-kernel basis) - Hopper has 64k (65536) registers per SM. These are allocated in fixed-size chunks of 256 registers.
Example - If a kernel uses 63 registers per thread
- Registers per warp = 63 * 32 = 2016
- Registers allocated per warp = 2048 (rounded up to nearest multiple of 256)
- Achievable active warps per SM = 65536 / 2048 = 32
- Occupancy = 32 / 64 = 50%
Hopper supports up to 64 warps per SM
If compiler needs more registers for a kernel than is allowed by the device/specified, then it spills to local memory.
Local memory is a thread-private storage space located in device memory and cached in L1 and L2. Local memory is at same level as global memory and hence slower.
In NCU, “Live Registers” metric can show hot-spots of high register usage.
Tips for reducing register pressure
-
__forceinlineto avoid function call overheads and the ABI - Tune loop unrolling - excessive unrolling can lead to excessive register usage
- Avoid 64-bit types wherever possible as they use two registers
- Check buffers in register if they can be moved to some other memory space (e.g. shared memory)
- Assign less work to individual threads
- Doing kernel fusion can also lead to increased register pressure
Occupancy Limiters - Thread Block size
Thread block size is a multiple of warp size (32). Even if you request fewer threads, hardware will round it up to the nearest multiple of 32.
Each thread block can have a maximum size of 1024.
Each SM in Hopper can have up to 64 warps, 32 blocks and 2048 threads.
Reducing Instruction Count
- Focus on all levels of the problem - source tweaks, algorithm changes, etc.
- Perform “inexpensive prechecks” to see if you can avoid expensive operations.
- Algebraic optimizations
- Operating in a different numeric space
- Use cccl for high performance primitives. Don’t reinvent the wheel.
- Vectorized instructions (memory operations, DPX, f32x2 on Blackwell)
E.g. for an instruction bound kernel -
- Making it float4 made it 128 bit loads
- Increase in shared memory traffic and decrease in instructions
- And since instruction bound -> better performance
Math Optimizations

Use the precision that is required. If lower precision is acceptable, then use it.
Beware of the implicit cast to double. Use the .f suffix on the numeric literals to avoid it.
Make use of the fast math optimizations - --use-fast-math
- Single Precision Intrinsics -
__cosf(),__expf(),__fsqrt_*__(), etc. - Single precision trigonometric math API functions may use some double precision instructions and local memory.

Algebraic Optimizations
Static Considerations
- Move divisors to the other side of comparison operators (division is expensive)
- If you have division by a run time constant, compute inverse on host and pass to kernel to multiply.
- Use template parameters for any variable known at compute time or with a limited range of values. Runtime compilation can take this even further.
Runtime Considerations
If possible, provide the compiler with hints which the user knows about e.g., the possible range of values produced by an expression and figure out if any optimizations are possible.
Interesting Example - Use signed integers rather than unsigned integers as loop counters. Reason - unsigned int overflows are defined behavior and the compiling needs to account for this resulting in possible extra instructions. Since int overflows are undefined behavior, the compiler has more flexibility to generate faster code.
Operating in a different numeric space
- Use log probabilities for improved accuracy and performance
- Comparing squared distances rather than distances to avoid
sqrt
Optimizing polynomial evaluation
- Use Horner’s method for polynomial evaluation.
- Take care of precision using the
.fsuffix on numeric literals. - Use
__fma()for polynomial evaluation. - Use
__fmaf()for single precision polynomial evaluation. - Or use
fmad=Truein the compiler flags.



Tensor Cores Overview
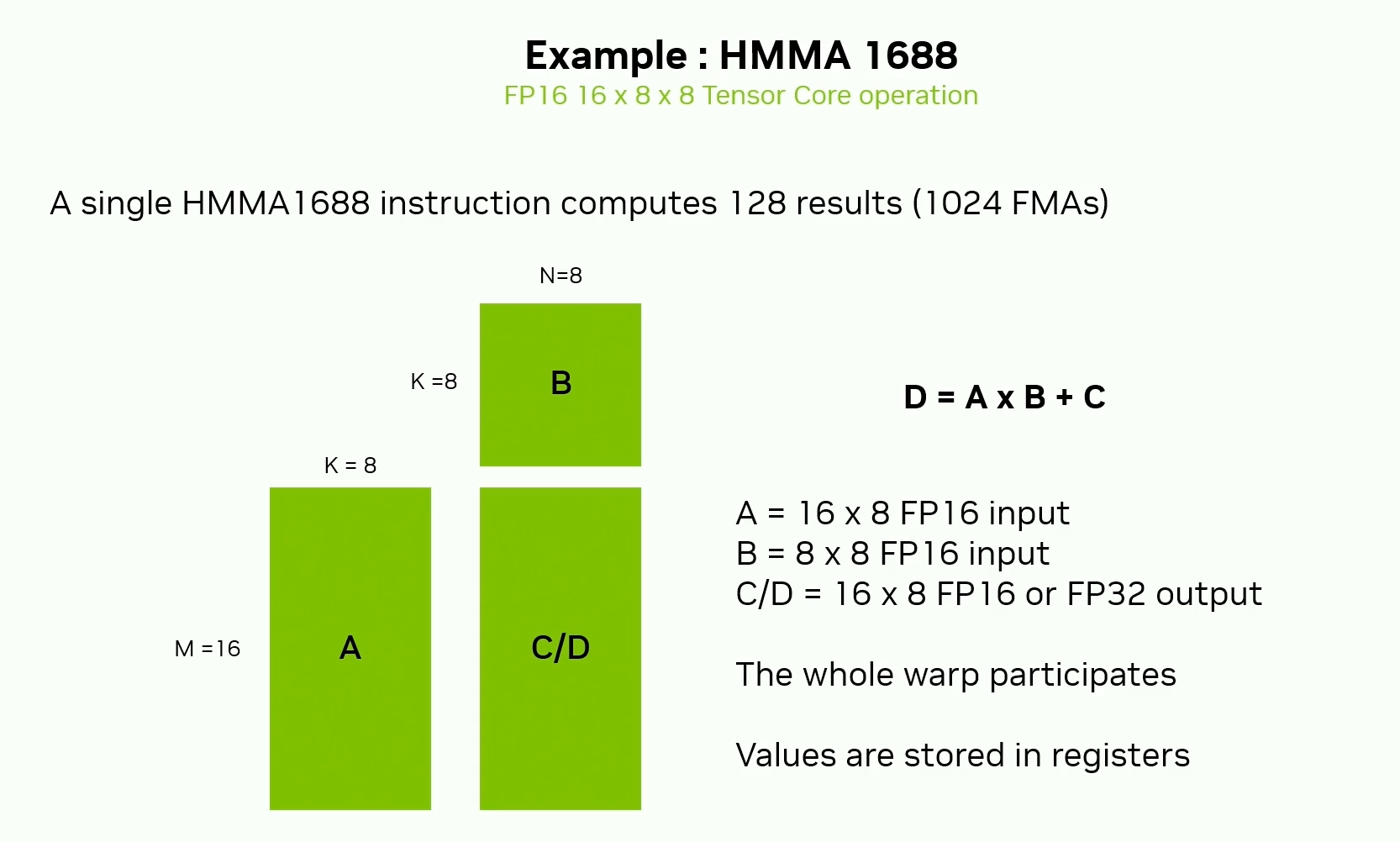
A, B, C will be distributed among the registers of the warp
History of Tensor Cores

Tensor Core Providers
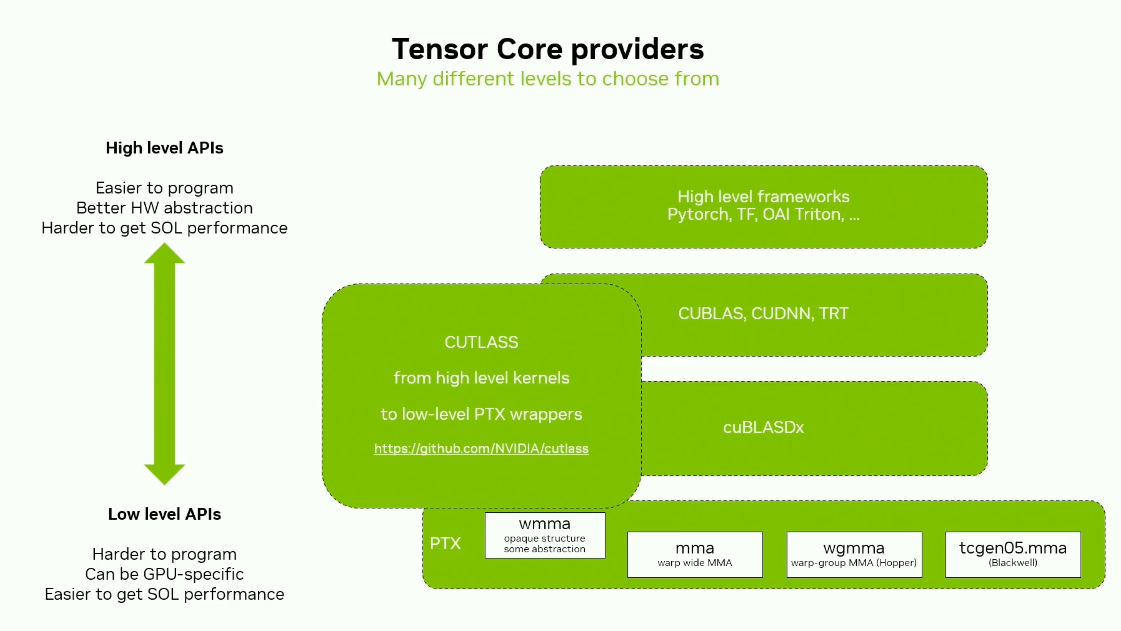
Hope this was helpful!