Deriving the Gradient for the Backward Pass of Layer Normalization
Forward Pass Recap
First, let’s write down the forward pass for a single input vector \(x\) (a row from \(X\)) of dimension \(N\):
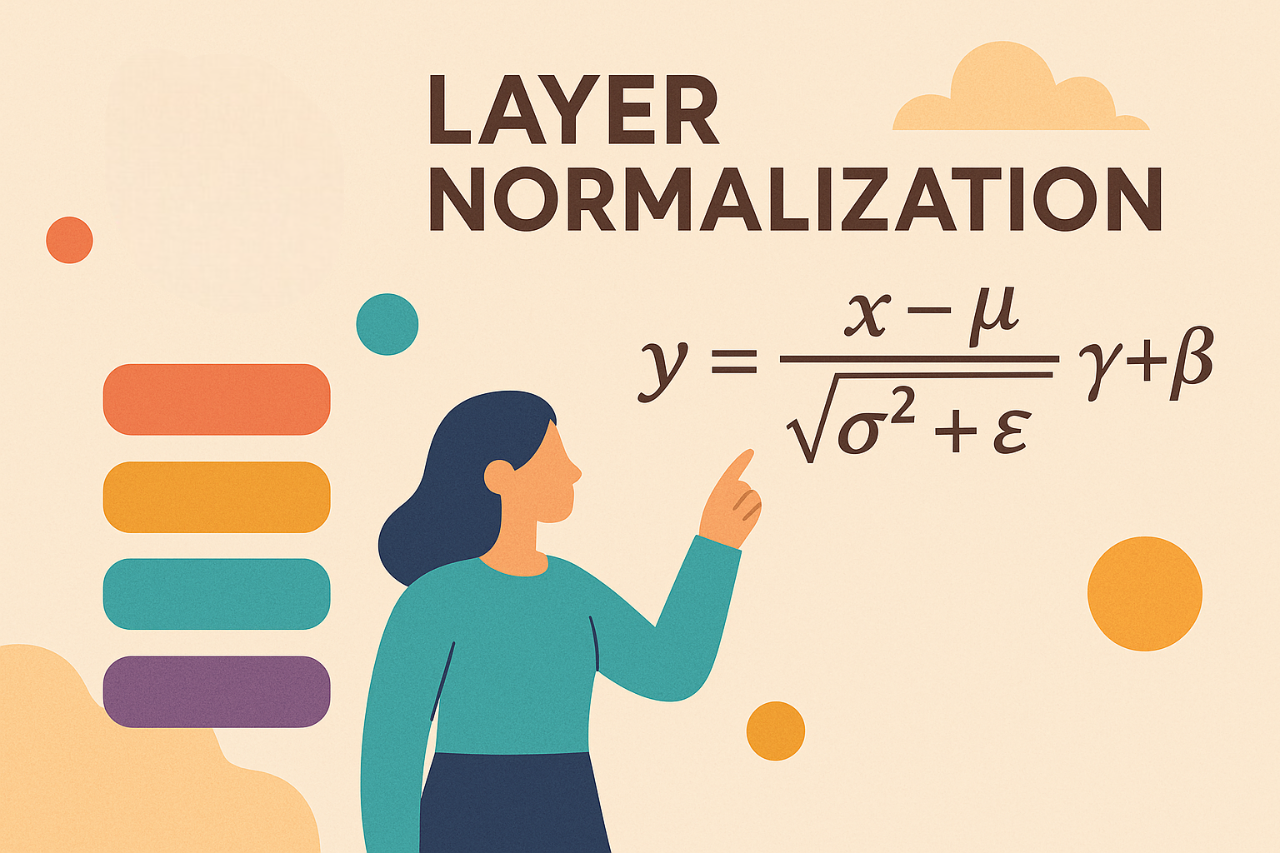
\[y = \frac{x - \mu}{\sqrt{\sigma^2 + \epsilon}} * \gamma + \beta\]We can break down the forward pass into the following steps:
- Mean: \(\mu = \frac{1}{N} \sum_j x_j\)
- Variance: \(\sigma^2 = \frac{1}{N} \sum_j (x_j - \mu)^2\)
- Inverse Standard Deviation (rstd): \(\text{rstd} = \frac{1}{\sqrt{\sigma^2 + \epsilon}}\)
- Normalized Input (\(\hat{x}\)): \(\begin{equation} \hat{x}_j = (x_j - \mu) \cdot \text{rstd} \label{eq:1} \end{equation}\)
- Output (\(y\)): \(\begin{equation} y_j = \hat{x}_j \cdot \gamma_j + \beta_j \label{eq:2} \end{equation}\)
In general for ML applications, while doing the backward pass, we are given \(\frac{dL}{dy_j}\) (denoted as \(dy_j\)) which is the gradient of the loss \(L\) with respect to the output \(y_j\).
We want to find \(\frac{dL}{dx_j}\) (denoted \(dx_j\)), \(\frac{dL}{d\gamma_j}\) (denoted \(d\gamma_j\)), and \(\frac{dL}{d\beta_j}\) (denoted \(d\beta_j\)).
Gradients \(\frac{dL}{d\gamma_j}\) and \(\frac{dL}{d\beta_j}\)
These are the simplest. \(\gamma_j\) and \(\beta_j\) only affect \(y_j\) directly in the final step.
Let’s define \(\delta_{kj}\) as 1 if \(k=j\), and \(0\) otherwise.
\[\frac{\partial y_k}{\partial \gamma_j} = \hat{x}_j \delta_{kj}\] \[\frac{\partial y_k}{\partial \beta_j} = \delta_{kj}\]Using the chain rule:
\[\frac{dL}{d\gamma_j} = \sum_k \left( \frac{dL}{dy_k} \frac{\partial y_k}{\partial \gamma_j} \right) = \frac{dL}{dy_j} \frac{\partial y_j}{\partial \gamma_j} = dy_j \cdot \hat{x}_j\] \[\frac{dL}{d\beta_j} = \sum_k \left( \frac{dL}{dy_k} \frac{\partial y_k}{\partial \beta_j} \right) = \frac{dL}{dy_j} \frac{\partial y_j}{\partial \beta_j} = dy_j \cdot 1\]If we consider the whole batch (multiple rows), \(\gamma_j\) and \(\beta_j\) are shared. So, the gradients are summed over all rows \(i\):
\[\frac{dL}{d\gamma_j} = \sum_i (dy_{ij} \cdot \hat{x}_{ij})\] \[\frac{dL}{d\beta_j} = \sum_i dy_{ij}\]Gradient \(\frac{dL}{d\hat{x}_j}\)
From Equation \eqref{eq:2}:
\[\frac{\partial y_k}{\partial \hat{x}_j} = \gamma_j \delta_{kj}\]So,
\[\begin{equation} \frac{dL}{d\hat{x}_j} = \sum_k \left( \frac{dL}{dy_k} \frac{\partial y_k}{\partial \hat{x}_j} \right) = \frac{dL}{dy_j} \frac{\partial y_j}{\partial \hat{x}_j} = dy_j \cdot \gamma_j \label{eq:3} \end{equation}\]Gradient \(\frac{dL}{dx_j}\) (The Core Part)
This is the most complex part because \(x_j\) affects all \(\hat{x}_k\) in the same row through \(\mu\) and \(\text{rstd}\).
We need \(\frac{dL}{dx_j} = \sum_k \left( \frac{dL}{d\hat{x}_k} \frac{\partial \hat{x}_k}{\partial x_j} \right)\).
We already have \(\frac{dL}{d\hat{x}_k} = dy_k \cdot \gamma_k\) (from Equation \eqref{eq:3}). Let’s call this \(d\hat{x}'_k\).
Now we need \(\frac{\partial \hat{x}_k}{\partial x_j}\). Recall (from Equation \eqref{eq:1}), \(\hat{x}_k = (x_k - \mu) \cdot \text{rstd}\).
Using the product rule:
\(\frac{\partial \hat{x}_k}{\partial x_j} = \frac{\partial (x_k - \mu)}{\partial x_j} \cdot \text{rstd} + (x_k - \mu) \cdot \frac{\partial \text{rstd}}{\partial x_j}\).
Let’s find the intermediate derivatives:
\[\frac{\partial \mu}{\partial x_j} = \frac{1}{N}\] \[\frac{\partial (x_k - \mu)}{\partial x_j} = \frac{\partial x_k}{\partial x_j} - \frac{\partial \mu}{\partial x_j} = \delta_{kj} - \frac{1}{N}\]Next, \(\frac{\partial \text{rstd}}{\partial x_j}\):
\[\text{rstd} = (\sigma^2 + \epsilon)^{-\frac{1}{2}}\] \[\frac{\partial \text{rstd}}{\partial x_j} = -\frac{1}{2} (\sigma^2 + \epsilon)^{-\frac{3}{2}} \frac{\partial \sigma^2}{\partial x_j}\] \[\begin{equation} \frac{\partial \text{rstd}}{\partial x_j} = -\frac{1}{2} \text{rstd}^3 \frac{\partial \sigma^2}{\partial x_j} \label{eq:4} \end{equation}\]Now, \(\frac{\partial \sigma^2}{\partial x_j}\):
\[\sigma^2 = \frac{1}{N} \sum_p (x_p - \mu)^2\] \[\frac{\partial \sigma^2}{\partial x_j} = \frac{1}{N} \sum_p \left[ 2 (x_p - \mu) \cdot \frac{\partial (x_p - \mu)}{\partial x_j} \right]\] \[\frac{\partial \sigma^2}{\partial x_j} = \frac{2}{N} \sum_p \left[ (x_p - \mu) \cdot \left(\delta_{pj} - \frac{1}{N}\right) \right]\] \[\frac{\partial \sigma^2}{\partial x_j} = \frac{2}{N} \left[ (x_j - \mu)\left(1 - \frac{1}{N}\right) + \sum_{p \neq j} (x_p - \mu)\left(-\frac{1}{N}\right) \right]\] \[\frac{\partial \sigma^2}{\partial x_j} = \frac{2}{N} \left[ (x_j - \mu) - \frac{1}{N}(x_j - \mu) - \frac{1}{N}\sum_{p \neq j} (x_p - \mu) \right]\] \[\frac{\partial \sigma^2}{\partial x_j} = \frac{2}{N} \left[ (x_j - \mu) - \frac{1}{N}\sum_p (x_p - \mu) \right]\]Since \(\sum_p (x_p - \mu) = 0\), the second term vanishes.
\[\begin{equation} \frac{\partial \sigma^2}{\partial x_j} = \frac{2}{N} (x_j - \mu) \label{eq:5} \end{equation}\]Substitute back into Equation \eqref{eq:4}, \(\frac{\partial \text{rstd}}{\partial x_j}\):
\[\frac{\partial \text{rstd}}{\partial x_j} = \left(-\frac{1}{2}\right) \cdot \text{rstd}^3 \cdot \left(\frac{2}{N}\right) \cdot (x_j - \mu)\] \[\frac{\partial \text{rstd}}{\partial x_j} = -\frac{1}{N} \text{rstd}^3 (x_j - \mu)\] \[\frac{\partial \text{rstd}}{\partial x_j} = -\frac{1}{N} \text{rstd}^2 \cdot ((x_j - \mu) \cdot \text{rstd})\] \[\begin{equation} \frac{\partial \text{rstd}}{\partial x_j} = -\frac{1}{N} \text{rstd}^2 \hat{x}_j \label{eq:6} \end{equation}\]Now assemble \(\frac{\partial \hat{x}_k}{\partial x_j}\):
\[\frac{\partial \hat{x}_k}{\partial x_j} = \left(\delta_{kj} - \frac{1}{N}\right) \cdot \text{rstd} + (x_k - \mu) \cdot \left(-\frac{1}{N} \text{rstd}^2 \hat{x}_j\right)\] \[\frac{\partial \hat{x}_k}{\partial x_j} = \left(\delta_{kj} - \frac{1}{N}\right) \cdot \text{rstd} - \frac{1}{N} \cdot ((x_k - \mu) \cdot \text{rstd}) \cdot \text{rstd} \cdot \hat{x}_j\] \[\frac{\partial \hat{x}_k}{\partial x_j} = \left(\delta_{kj} - \frac{1}{N}\right) \cdot \text{rstd} - \frac{1}{N} \hat{x}_k \cdot \text{rstd} \cdot \hat{x}_j\] \[\begin{equation} \frac{\partial \hat{x}_k}{\partial x_j} = \frac{\text{rstd}}{N} (N \delta_{kj} - 1 - \hat{x}_k \hat{x}_j) \label{eq:7} \end{equation}\]Finally, using Equation \eqref{eq:7},
\[\frac{dL}{dx_j} = \sum_k \left( d\hat{x}'_k \cdot \frac{\partial \hat{x}_k}{\partial x_j} \right)\] \[\frac{dL}{dx_j} = \sum_k \left[ d\hat{x}'_k \cdot \frac{\text{rstd}}{N} (N \delta_{kj} - 1 - \hat{x}_k \hat{x}_j) \right]\] \[\frac{dL}{dx_j} = \frac{\text{rstd}}{N} \sum_k \left[ d\hat{x}'_k (N \delta_{kj} - 1 - \hat{x}_k \hat{x}_j) \right]\] \[\frac{dL}{dx_j} = \frac{\text{rstd}}{N} \left[ (d\hat{x}'_j (N - 1 - \hat{x}_j \hat{x}_j)) + \sum_{k \neq j} d\hat{x}'_k (-1 - \hat{x}_k \hat{x}_j) \right]\] \[\frac{dL}{dx_j} = \frac{\text{rstd}}{N} \left[ N d\hat{x}'_j - d\hat{x}'_j - d\hat{x}'_j \hat{x}_j^2 - \sum_{k \neq j} d\hat{x}'_k - \sum_{k \neq j} (d\hat{x}'_k \hat{x}_k \hat{x}_j) \right]\] \[\frac{dL}{dx_j} = \frac{\text{rstd}}{N} \left[ N d\hat{x}'_j - \left(\sum_k d\hat{x}'_k\right) - \hat{x}_j \left(\sum_k d\hat{x}'_k \hat{x}_k\right) \right]\]The sum expansions are correct because \(d\hat{x}'_j \hat{x}_j^2\) is one term of \(\hat{x}_j (\sum_k d\hat{x}'_k \hat{x}_k)\) and \(d\hat{x}'_j\) is one term of \(\sum_k d\hat{x}'_k\).
So, for a specific \(j\), from Equation \eqref{eq:8}:
\[\begin{equation} \frac{dL}{dx_j} = \text{rstd} \cdot \left[ d\hat{x}'_j - \frac{1}{N} \left(\sum_k d\hat{x}'_k\right) - \frac{\hat{x}_j}{N} \left(\sum_k d\hat{x}'_k \hat{x}_k\right) \right] \label{eq:8} \end{equation}\]Now:
- \(d\hat{x}'_j = dy_j \cdot \gamma_j\) (from Equation \eqref{eq:3})
- Let \(c_2 = \frac{1}{N} \sum_k d\hat{x}'_k = \frac{1}{N} \sum_k (dy_k \cdot \gamma_k)\)
- Let \(c_1 = \frac{1}{N} \sum_k (d\hat{x}'_k \cdot \hat{x}_k) = \frac{1}{N} \sum_k ( (dy_k \cdot \gamma_k) \cdot \hat{x}_k )\)
Substituting these back in Equation \eqref{eq:8}:
\[\frac{dL}{dx_j} = \text{rstd} \cdot \left[ (dy_j \cdot \gamma_j) - c_2 - \hat{x}_j \cdot c_1 \right]\] \[\begin{equation} \frac{dL}{dx_j} = \text{rstd} \cdot \left[ (dy_j \cdot \gamma_j) - (\hat{x}_j \cdot c_1 + c_2) \right] \label{eq:9} \end{equation}\]If we want to be more explicit with batch indexing (let \(i\) be the row/sequence index in the batch):
\[\begin{equation} \frac{dL}{dx_{ij}} = \text{rstd}_i \cdot \left[ (dy_{ij} \cdot \gamma_j) - c_{2_{i}} - \hat{x}_{ij} \cdot c_{1_{i}} \right] \label{eq:10} \end{equation}\]We now have the final gradients -
\[\boxed{ \begin{aligned} \frac{dL}{d\gamma_j} &= \sum_i (dy_{ij} \cdot \hat{x}_{ij}) \\ \frac{dL}{d\beta_j} &= \sum_i dy_{ij} \\ \frac{dL}{dx_{ij}} &= \text{rstd}_i \cdot \left[ (dy_{ij} \cdot \gamma_j) - c_{2_{i}} - \hat{x}_{ij} \cdot c_{1_{i}} \right] \end{aligned} }\]where,
\[\boxed{ \begin{aligned} c_1 = \frac{1}{N} \sum_k (d\hat{x}'_k \cdot \hat{x}_k) &= \frac{1}{N} \sum_k ( (dy_k \cdot \gamma_k) \cdot \hat{x}_k ) \\ c_2 = \frac{1}{N} \sum_k d\hat{x}'_k &= \frac{1}{N} \sum_k (dy_k \cdot \gamma_k) \\ d\hat{x}'_j &= dy_j \cdot \gamma_j \end{aligned} }\]Hope this was helpful!