Understanding Multi-Head Latent Attention (MLA)
Code - https://github.com/shreyansh26/multihead-latent-attention
Deepseek introduced Multi-Head Latent Attention (MLA) in the Deepseek-v2 paper as a way to improve the efficiency of attention computation during inference by reducing the KV cache bottleneck. MLA achieves better performance than Multi-Head Attention (MHA).
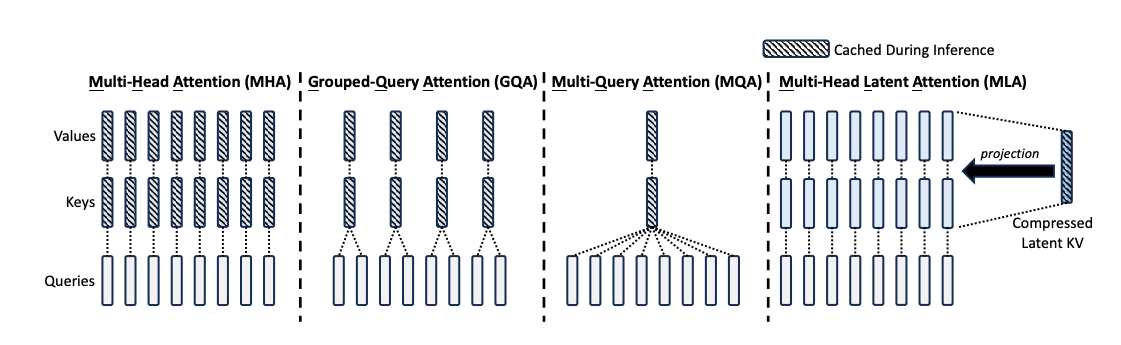
Grouped-Query Attention (GQA) and Multi-Query Attention (MQA) reduce Key/Value (KV) duplication, shrinking the KV cache and cutting bandwidth. Multi-Head Latent Attention (MLA) goes further: it introduces a low-rank latent space that factorizes attention, enabling both efficient training and extremely efficient inference with a simple algebraic “absorption” trick.
This post walks from MHA → GQA → MQA → MLA, then shows the fusion and absorption optimizations, with concrete PyTorch code and equations you can render in Markdown.
Revisiting Multi-Head Attention (MHA)
MHA projects input tokens into per-head Query/Key/Value, computes attention per head, then merges:
Given hidden size (D), number of heads (H), and head dimension (d) where (D = H \cdot d):
- Queries: \(Q \in \mathbb{R}^{B \times S \times H \times d}\)
- Keys: \(K \in \mathbb{R}^{B \times S \times H \times d}\)
- Values: \(V \in \mathbb{R}^{B \times S \times H \times d}\)
- Attention per head: \(\mathrm{Attn}(Q_i, K_i, V_i) = \mathrm{Softmax}\!\left(\frac{Q_i K_i^\top}{\sqrt{d}}\right) V_i\)
Code reference (simplified from our mha.py):
def forward(self, x_bsd, is_causal=False, kv_cache=None, return_torch_ref=False):
batch_size, seq_len, d_model = x_bsd.shape
new_shape = (batch_size, seq_len, -1, self.head_dim)
q_bsqh = self.q_proj(x_bsd).view(new_shape)
k_blkh = self.k_proj(x_bsd).view(new_shape)
v_blkh = self.v_proj(x_bsd).view(new_shape)
q_bsqh = apply_rotary_emb(q_bsqh, self.freqs_cis)
k_blkh = apply_rotary_emb(k_blkh, self.freqs_cis)
q_bqsh = q_bsqh.transpose(1, 2)
k_bklh = k_blkh.transpose(1, 2)
v_bklh = v_blkh.transpose(1, 2)
out_bsd = naive_attention(q_bqsh, k_bklh, v_bklh, is_causal=is_causal)
out_bsd = self.o_proj(out_bsd)
return out_bsd
Inefficiency: we compute and store (K,V) per head. For long sequences, the KV cache dominates memory and communication.
GQA: Grouped-Query Attention
GQA shares Keys/Values across groups of query heads: \(H\) query heads share \(H_\text{kv}\) KV heads (with \(H_\text{kv} < H\)). Complexity and KV cache both drop by a factor of \(H / H_\text{kv}\) compared to MHA, while preserving multiple query heads for expressivity.
Trade-off: less KV diversity per query head; often negligible loss in modeling capacity with slight improvement in inference efficiency.
MQA: Multi-Query Attention
MQA goes to the limit: one shared KV head for all queries \(H_\text{kv}=1\). KV cache drops by \(\approx H\times\) versus MHA; cross-device communication shrinks markedly. For long-context inference, this is a big win.
Downside: a single KV head may reduce modeling capacity if used naïvely. MLA addresses this by introducing a low-rank latent structure that preserves expressivity while keeping runtime costs low.
MLA: Multi-Head Latent Attention
MLA factorizes attention via low-rank latent projections. Notation follows our reference:
- Latent compression:
where \(W^{DKV} \in \mathbb{R}^{r_{kv} \times D}\), \(W^{DQ} \in \mathbb{R}^{r_q \times D}\).
- Per-head decompression:
where \(W^{UK} \in \mathbb{R}^{\text{nh}_{kv} * d_{\text{qk}_{nope}} \times r_{kv}}\), \(W^{UV} \in \mathbb{R}^{\text{nh}_{kv} * d_v \times r_{kv}}\), \(W^{UQ} \in \mathbb{R}^{\text{nh}_{q} * d_{\text{qk}_{nope}} \times r_{q}}\).
- Decoupled RoPE:
where \(W^{KR} \in \mathbb{R}^{d_{\text{qk}_{rope}} \times D}\), \(W^{QR} \in \mathbb{R}^{\text{nh}_{q} * d_{\text{qk}_{rope}} \times r_{q}}\).
and we concatenate for each head (i):
\[\mathbf{k}_{t,i} = [\,\mathbf{k}^N_{t,i};\ \mathbf{k}^R_t\,],\qquad \mathbf{q}_{t,i} = [\,\mathbf{q}^N_{t,i};\ \mathbf{q}^R_{t,i}\,].\]The forward in our MLA implementation mirrors this shape construction:
# MLA.forward (selected lines)
c_kv = self.w_dkv(x_bsd) # [B, S, r_kv]
c_q = self.w_dq(x_bsd) # [B, S, r_q]
k_r = self.w_kr(x_bsd) # [B, S, dR]
k_r = k_r.view(batch_size, seq_len, 1, self.qk_rope_head_dim)
k_r = apply_rotary_emb(k_r, self.freqs_cis_qk).transpose(1, 2) # [B, 1, S, dR]
if cache is not None:
c_kv = cache.compressed_kv.update(c_kv) # [B, S_kv, r_kv]
k_r = cache.k_rope.update(k_r) # [B, 1, S_kv, dR]
k_n = self.w_uk(c_kv).view(batch_size, seq_len_kv, self.num_key_value_heads, self.qk_nope_head_dim)
k_n = k_n.transpose(1, 2) # [B, H_kv, S_kv, dN]
k = torch.cat([k_r.repeat_interleave(self.num_key_value_heads, dim=1), k_n], dim=-1)
q_r = self.w_qr(c_q).view(batch_size, seq_len, self.num_attention_heads, self.qk_rope_head_dim)
q_r = apply_rotary_emb(q_r, self.freqs_cis_qk).transpose(1, 2) # [B, H, S, dR]
q_n = self.w_uq(c_q).view(batch_size, seq_len, self.num_attention_heads, self.qk_nope_head_dim).transpose(1, 2)
q = torch.cat([q_r, q_n], dim=-1)
v = self.w_uv(c_kv).view(batch_size, seq_len_kv, self.num_key_value_heads, self.v_head_dim).transpose(1, 2)
out = sdpa_attention(q, k, v, is_causal=is_causal)
out = self.w_o(out)
Intuition: MLA maintains multi-head queries, but routes them through a shared latent bottleneck for \((K,V)\) (and optionally for parts of \(Q\)). This preserves per-head specialization via \(W^{UQ}\), \(W^{UK}\), \(W^{UV}\), while dramatically reducing the “surface area” of the KV cache.
Fusion: fewer intermediate tensors, same math
We can fuse linears to reduce memory traffic:
- Combine \(W^{DKV}\) and \(W^{KR}\) into a single projection (
w_dkv_kr). - Combine \(W^{UK}\) and \(W^{UV}\) into a single projection (
w_uk_uv) then split. - Combine \(W^{QR}\) and \(W^{UQ}\) into a single projection (
w_qr_uq) then split for \(\mathbf{q}^N\) and \(\mathbf{q}^C\).
Snippet from MLAFused.forward:
c_q = self.w_dq(x_bsd) # [B, S, r_q]
c_kv_kr = self.w_dkv_kr(x_bsd) # [B, S, r_kv + dR]
c_kv, k_r = torch.split(c_kv_kr, [self.kv_lora_rank, self.qk_rope_head_dim], dim=-1)
k_r = apply_rotary_emb(k_r.view(batch_size, seq_len, 1, self.qk_rope_head_dim), self.freqs_cis_qk).transpose(1, 2)
if cache is not None:
c_kv = cache.compressed_kv.update(c_kv)
k_r = cache.k_rope.update(k_r)
k_n_v = self.w_uk_uv(c_kv) # [B, S_kv, H_kv * (dN + dV)]
k_n, v = torch.split(k_n_v, [self.num_key_value_heads * self.qk_nope_head_dim,
self.num_key_value_heads * self.v_head_dim], dim=-1)
# reshape, build k, build q via w_qr_uq, attend, project out...
Fusion preserves semantics but minimizes reads/writes of large intermediate tensors—especially important under long sequence lengths where bandwidth dominates.
Absorption: inference-time MQA with latent routing
At inference we can algebraically “absorb” \(W^{UK}\) into the query path and \(W^{UV}\) into the output path. Starting with
\[\mathbf{q}_{t,i} = [\,\mathbf{q}^C_{t,i}; \mathbf{q}^R_{t,i}\,],\qquad \mathbf{k}_t = [\,\mathbf{k}^C_t;\ \mathbf{k}^R_t\,],\]define
\[\hat{\mathbf{q}}_{t,i} = \big[(W^{UK}_i)^\top \mathbf{q}^C_{t,i};\ \mathbf{q}^R_{t,i}\big],\qquad \hat{\mathbf{k}}_t = \big[\mathbf{c}^{KV}_t;\ \mathbf{k}^R_t\big].\]Then attention can be computed against a single shared latent KV head \(\mathbf{c}^{KV}\) (plus shared RoPE key), and the per-head value projection is postponed to the output:
\[\hat{\mathbf{o}}_{t,i} = \sum_{j=1}^{t} \mathrm{softmax}_j\!\left(\frac{\hat{\mathbf{q}}_{t,i}^\top \hat{\mathbf{k}}_j}{\sqrt{d + d^R}}\right) \mathbf{c}^{KV}_j,\quad \mathbf{y}_t = W^{O} \,[\, W^{UV}_1 \hat{\mathbf{o}}_{t,1};\dots; W^{UV}_H \hat{\mathbf{o}}_{t,H}\,].\]Our MLAFusedAbsorbed implements exactly this MQA-like inference path:
# Keys: single shared head [k_r, c_kv]
k = torch.cat([k_r, c_kv.unsqueeze(1)], dim=-1) # [B, 1, S_kv, dR + r_kv]
# Queries: per-head RoPE + absorbed-nope to r_kv
q_r = self.w_qr(c_q).view(batch_size, seq_len, self.num_attention_heads, self.qk_rope_head_dim)
q_r = apply_rotary_emb(q_r, self.freqs_cis_qk).transpose(1, 2)
q_n = self.w_uq_absorbed(c_q).view(batch_size, seq_len, self.num_attention_heads, self.kv_lora_rank).transpose(1, 2)
q = torch.cat([q_r, q_n], dim=-1)
# Values: the shared latent c_kv as single head
v = c_kv.unsqueeze(1) # [B, 1, S_kv, r_kv]
out = sdpa_attention(q, k, v, is_causal=is_causal) # MQA-like compute
out = self.w_o_absorbed(out) # absorbs W^{UV} into W^O
Effect: KV cache stores \(\mathbf{c}^{KV}\) once per token (plus a small shared RoPE key). Communication is essentially MQA, but per-head specialization is retained via the absorbed query/output linears.
Complexity and KV cache discussion
Let:
- \(B\): batch size, \(S\): sequence length, \(H\): attention heads,
- \(H_{kv}\): KV heads in GQA/MLA, \(d\): head dim, \(d_{\text{qk}_{rope}}\): RoPE dim,
- \(r_q, r_{kv}\): low-rank dimensions for query/kv latents.
Rough per-token storage for the KV cache (ignoring dtype constants):
- MHA: \(O(H \cdot S \cdot d)\) for \(K\) and \(O(H \cdot S \cdot d)\) for \(V\).
- GQA: \(O(H_{kv} \cdot S \cdot d)\) per \(K,V\).
- MQA: \(O(S \cdot d)\) per \(K,V\).
- MLA: \(O(S \cdot r_{kv})\) for \(\mathbf{c}^{KV}_t\) and \(O(S \cdot d_{\text{qk}_{rope}})\) for \(\mathbf{k}^R_t\)
Communication between devices during decode scales with KV cache size too; MLA’s absorbed path therefore inherits MQA’s excellent scaling while maintaining multi-head query diversity.
Compute:
- Matmuls with \(W^{DKV}\) and \(W^{DQ}\) are shared per token, independent of \(H\).
- Per-head expansions via \(W^{UQ}, W^{UK}, W^{UV}\) are relatively cheap when \(r_q, r_{kv} \ll D\).
- Absorption swaps some inner-loop per-token head matmuls for outer-loop linears, keeping the high-arithmetic-intensity parts in efficient GEMMs.
KV Cache storage size comparison
MLA has to cache \(\mathbf{c}^{KV}\) and \(\mathbf{k}^R\) for each token, which is \(r_{kv} + d_{\text{qk}_{rope}}\) per token. In the Deepseek v2 and v3 configs, \(r_{kv} = 4 d_{\text{qk}_{nope}}\) and \(d_{\text{qk}_{rope}} = 0.5 * d_{\text{qk}_{nope}}\).
The table below shows the KV cache size comparison for the different attention mechanisms.
| Attention Mechanism | KV Cache per Token |
|---|---|
| MHA | \(2n_h d_h l\) |
| GQA | \(2n_g d_h l\) |
| MQA | \(2d_h l\) |
| MLA | \((r_{kv} + d_{\text{qk}_{rope}}) l \approx \frac{9}{2} d_{\text{qk}_{nope}} l\) |
Conclusion
MLA reframes attention as a low-rank routing problem. During training, it behaves much like GQA but with smaller activations; during inference, absorption yields an MQA-like footprint with per-head specialization preserved through the query/output paths. If your production bottleneck is KV cache size or cross-device bandwidth, MLA’s absorbed path is a direct drop-in to claw back latency without sacrificing modeling power.
These are my notes on MLA and hopefully it proves useful to someone looking to understand MLA better.
Here is the code - https://github.com/shreyansh26/multihead-latent-attention